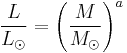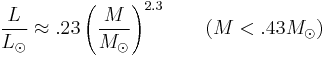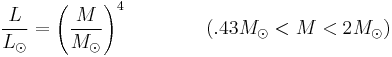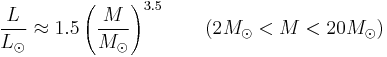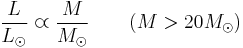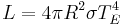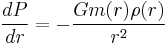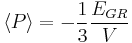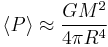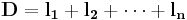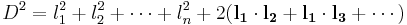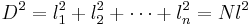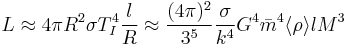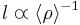Mass–luminosity relation
In astrophysics, the mass–luminosity relation is an equation giving the relationship between a star's mass and its luminosity. The relationship is represented by the equation:
where L⊙ and M⊙ are the luminosity and mass of the sun and 1 < a < 6.[1] The value a = 3.5 is commonly used for main-sequence stars.[2] This equation and the usual value of a = 3.5 only applies to main-sequence stars with masses 2M⊙ < M < 20M⊙ and does not apply to red giants or white dwarfs.
In summary, the relations for stars with different ranges of mass are to good approximation the following:[1][3]
For stars with masses less than .43M⊙, convection is the sole energy transport process, so the relation changes significantly. For stars with masses M > 20M⊙ the relationship flattens out and becomes L ∝ M.[1] It can be shown this change is due to an increase in radiation pressure in massive stars.[1] These equations are determined empirically by determining the mass of stars in binary systems to which the distance is known via standard parallax measurements or other techniques. After enough stars are plotted, stars will form a line on a logarithmic plot and slope of the line gives the proper value of a.
The mass–luminosity relation is important because it can be used to find the distance to binary systems which are too far for normal parallax measurements, using a technique called "dynamical parallax".[4] In this technique, the masses of the two stars in a binary system are estimated, usually as being the mass of the sun. Then, using Kepler's laws of celestial mechanics, the distance between the stars is calculated. Once this distance is found, the distance away can be found via the arc subtended in the sky, giving a preliminary distance measurement. From this measurement and the apparent magnitudes of both stars, the luminosities can be found, and by using the mass–luminosity relationship, the masses of each star. These masses are used to re-calculate the separation distance, and the process is repeated. The process is iterated many times, and accuracies as high as 5% can be achieved.[4] The mass–luminosity relationship can also be used to determine the lifetime of stars by noting that lifetime is approximately proportional to M/L. One finds that more massive stars live shorter. A more sophisticated calculation factors in a star's loss of mass over time.
Derivation
Deriving a theoretically exact mass–luminosity relation requires finding the energy generation equation and building a thermodynamic model of the inside of a star. However, the basic relation L ∝ M3 can be derived using some basic physics and simplifying assumptions.[5] The first such derivation was performed by astrophysicist Arthur Eddington in 1924.[6] The derivation showed that stars can be approximately modelled as ideal gasses, which was a new, somewhat radical idea at the time. What follows is very similar to Eddington's approach, but uses a random-walk analysis and does not include the optical opacity.
To the first approximation, stars are black body radiators with a surface area of 4πR2. Thus, from the Stefan-Boltzmann law we find that the luminosity (energy emitted per second) is
Where σ is Stefan's constant, 5.67 × 10−8W m−2 K−4.
Under the condition of hydrostatic equilibrium,
By integrating both sides of this relation from r = 0 to r = R, one arrives at a form of the virial theorem:
The potential energy of a spherical mass distribution is 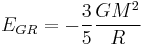 . This and the volume are substituted in to give:
. This and the volume are substituted in to give:
Simplifying greatly, we next use the ideal gas law (PV = nkT) to solve for the temperature.
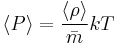
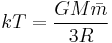 .
.
Here 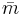 is the average mass of gas particles within the star. Now, we can substitute this equation into the initial luminosity equation, along with
is the average mass of gas particles within the star. Now, we can substitute this equation into the initial luminosity equation, along with
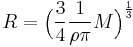 to arrive at
to arrive at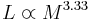
A slightly more exact result can be achieved by considering that the above equation gives the average temperature based on the average pressure, but what is actually needed is the surface temperature. Because stars are much hotter in the center then near the surface, we next need to estimate the relationship between the surface temperature and internal temperature. The center is so much hotter since energy takes a long time to escape, otherwise, thermodynamic equilibrium would be achieved quickly and the temperature would be nearly uniform throughout. We can use a random walk analysis to estimate the "delay factor", ie. the amount of time it takes energy to escape. We let 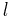 represent the mean free path for a photon within the sun. In actuality, the mean free path depends on the density and temperature, but here it will be approximated as a constant. After N interactions, resulting in N vector displacements in random directions, the distance traveled is:
represent the mean free path for a photon within the sun. In actuality, the mean free path depends on the density and temperature, but here it will be approximated as a constant. After N interactions, resulting in N vector displacements in random directions, the distance traveled is:
The square of the net displacement is:
If we average over many random direction changes, the terms involving dot products cancel because the direction is random. Hence, for large  ,
,
Thus, to escape from the sun, on average 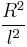 steps are required. The time this takes is
steps are required. The time this takes is 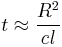 . In contrast, the time to escape directly out of the sun from the center is
. In contrast, the time to escape directly out of the sun from the center is 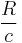 , which is a factor of
, which is a factor of 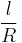 shorter.
shorter.
Thus, factoring this into the Stefan-Boltzmann law, we find
![T_E\approx \Big[ \frac{l}{R}\Big]^{\frac{1}{4}}T_I](/2012-wikipedia_en_all_nopic_01_2012/I/8f61845449b4ba749af82a51743d64bc.png) .
.
Thus, combining the above equations, we find that[5]
But the mean free path is inversely proportional to the product of the cross section and the numerical density, and thus
which gives
Distinguishing between small and large stellar masses
One may distinguish between the cases of small and large stellar masses by deriving the above results using radiation pressure. In this case, it is easier to use the optical opacity  and to consider the internal temperature TI directly; more precisely, we consider the average temperature in the radiation zone.
and to consider the internal temperature TI directly; more precisely, we consider the average temperature in the radiation zone.
We begin by noting a relation between the radiation pressure Prad and luminosity. The gradient of radiation pressure is equal to the momentum transfer absorbed from the radiation, giving:
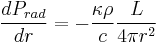
where c is the velocity of light. Note that 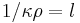 , the photon mean free path.
, the photon mean free path.
The radiation pressure is related to the temperature by 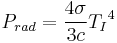 , so we have
, so we have
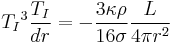
from which it follows directly that
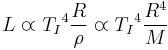 .
.
In the radiation zone gravity is balanced by the pressure on the gas coming from both itself (approxiamted by ideal gas pressure) and from the radiation. For a small enough stellar mass the latter is negligible and one arrives at
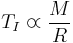
as before. More precisely, since we integrated from 0 to R we have 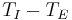 on the left side, but we may neglect the surface temperature TE with respect to the internal temperature TI.
on the left side, but we may neglect the surface temperature TE with respect to the internal temperature TI.
From this it follows directly that
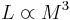
For a large enough stellar mass, the radiation pressure is larger than the gas pressure in the radiation zone. Plugging the radiation pressure instead of the ideal gas pressure we used above, we get:
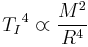
hence
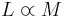
References
- ^ a b c d Salaris, Maurizio; Santi Cassisi (2005). Evolution of stars and stellar populations. John Wiley & Sons. pp. 138–140. ISBN 0470092203. http://books.google.com/books?id=r1dNzr8viRYC&lpg=PA138&dq=Mass-Luminosity%20relation&lr=&client=firefox-a&pg=PA138#v=onepage&q=&f=false.
- ^ "Mass-luminosity relationship". Hyperphysics. http://hyperphysics.phy-astr.gsu.edu/hbase/Astro/herrus.html#c3. Retrieved 2009-08-23.
- ^ Duric, Nebojsa (2004). Advanced astrophysics. Cambridge University Press. pp. 19. ISBN 9780521525718. http://books.google.com/books?id=-ljdYMmI0EIC&lpg=PA19&ots=VdMUIiCdP_&dq=Mass-luminosity%20relation&pg=PA19#v=onepage&q=&f=false.
- ^ a b Mullaney, James (2005). Double and multiple stars and how to observe them. Springer. ISBN 1852337516. http://books.google.com/books?id=OM3hozlKt9AC&lpg=PA27&ots=da06NVpIY_&dq=Mass-Luminosity%20relation%20distance%20binary&pg=PA27#v=onepage&q=&f=false.
- ^ a b Phillips, A.C. (1999). The Physics of Stars. John Wiley & Sons. ISBN 9780471987987.
- ^ Lecchini, Stefano. How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation. Bern Studies in the History and Philosophy of Science. ISBN 9783952288269. http://philoscience.unibe.ch/bern-studies/how-dwarfs-became-giants-the-discovery-of-the-mass-luminosity-relation.